05.04.25

The Derivative

Slopes of a function

Lets consider a simple function like this

def f(x):

return 3*x**2-4*x+5

xs = np.arange(-5,5,0.25)
ys = f(xs)
plt.plot(xs,ys)
plt.show()

The output of which looks like this:

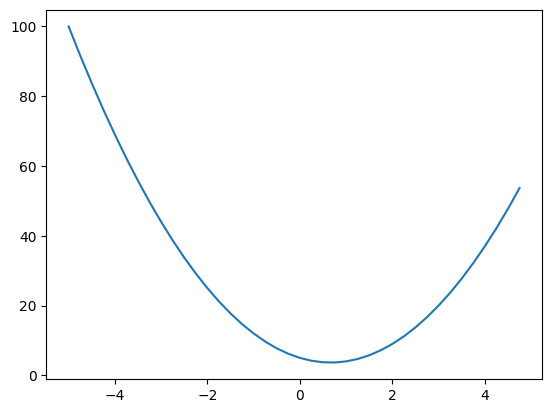
Derivative of a single input function

What is the meaning of the derivative?
A derivative essentially measure the sensitivity of a function to a small change in its input.

Let's illustrate it with an example

h = 0.001
x = 3.0
f(x+h)

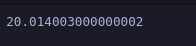
In the example given above, for a small change h = 0.001 in the input of 3.0, how would the function values change? It should be slightly greater as indicated by the graph, which shows a steeper slope. the function is going up from the x value 2.

What changes when the input becomes neagtive? how do the magnitude and the direction of the slope change?

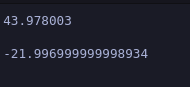
From the graph, x values in the negative direction have greater values, hence the magnitude is larger, but in that region, the slope is decreasing, hence the derivative is -ve and higher

h = 0.001
x = - 3.0
print(f(x+h))

slope = (f(x+h)-f(x))/h
slope

Derivatives of function with multiple inputs

This will be our set of parameters

a = 2.0
b = -3.0
c = 10.0
  
d = a*b+c #this is our function
print(d)

Applying a small change the value of a

h = 0.0001
a = 2.0
b = -3.0
c = 10.0

d1 = a*b+c
a+=h
d2 = a*b+c

  

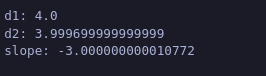
print(f"d1: {d1}")
print(f"d2: {d2}")-
print(f"slope: {(d2-d1)/h}")

What happened here?
When the change to a was made, the derivatives w.rt a would mean that the value of b, would naturally dominate; since d(ab+c)/da = b. So as the value of b is -3, the value of the slope that we got is also close to -3.

Applying a small change to b

h = 0.0001
a = 2.0
b = -3.0
c = 10.0

d1 = a*b+c
b+=h
d2 = a*b+c

  

print(f"d1: {d1}")
print(f"d2: {d2}")-
print(f"slope: {(d2-d1)/h}")

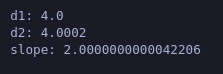
What happened here?
Now in this case taking the derivative would get us a value of a, which is what our slope calculation got us, which is 2.

Applying a small change to c

h = 0.0001
a = 2.0
b = -3.0
c = 10.0

d1 = a*b+c
c+=h
d2 = a*b+c

  

print(f"d1: {d1}")
print(f"d2: {d2}")-
print(f"slope: {(d2-d1)/h}")

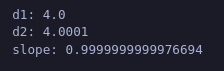
What happened here?
Now that we are differentiating w.r.t to c, as c is a contant the value of the expression would collapse down to 1, hence the answer of 0.999 which is approx. 1.

Read the next chapter here: Chapter 2-Building micrograd